Co to są liczby pierwsze i jakie jest ich zastosowanie? Liczby pierwsze do 100

Liczby pierwsze to zagadnienie, które od stuleci zaprząta głowy matematyków. Od momentu, gdy w IV wieku p.n.e. Euklides dowiódł, że liczb pierwszych jest nieskończenie wiele, naukowcy nieustannie starają się odkrywać kolejne z nich. Sprawdź, co warto wiedzieć o liczbach pierwszych i poznaj ciekawostki, które się z nimi wiążą!

Czym są liczby pierwsze i liczby złożone?

Liczba pierwsza to liczba naturalna, która jest podzielna tylko przez 1 i przez samą siebie.

Poza liczbami pierwszymi istnieją również liczby złożone, czyli liczby, której mają więcej niż dwa dzielniki. Liczbę złożoną można podzielić przez 1, samą siebie oraz przez co najmniej jeszcze jedną inną liczbę.

Liczba złożona może zostać zapisana w postaci iloczynu mniejszych liczb naturalnych, np. 8=4·2. Liczby pierwsze nie mogą zostać zapisane w taki sposób.

Liczby pierwsze do 100

Liczb pierwszych jest bardzo dużo – wśród liczb mniejszych od 100 jest ich 25. Oto one:

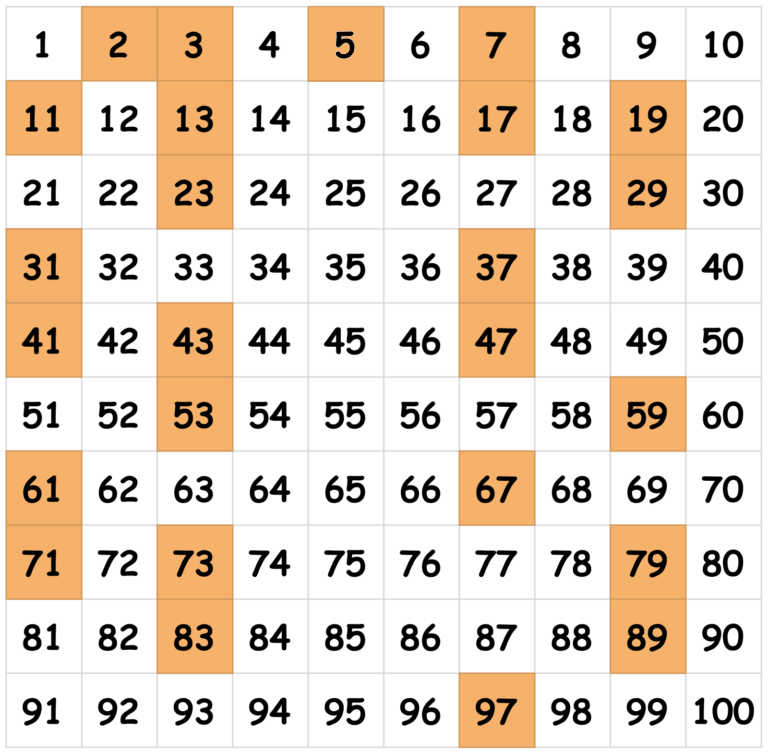
Liczb pierwszych, które są mniejsze od 1000, jest 168. Wśród liczb stucyfrowych (sic!) jedna na trzysta liczb złożonych jest liczbą pierwszą. A co dalej? Niestety, wciąż nie opracowano uniwersalnego wzoru, który pozwalałby odnajdywać kolejne liczby pierwsze. Ciekawostka
Od 1996 roku prowadzony jest projekt Great Internet Mersenne Prime Search, którego celem jest odkrywanie kolejnych liczb pierwszych. Od momentu rozpoczęcia projektu do dzisiaj – czyli w ciągu 26 lat – odkryto 16 nowych liczb pierwszych. Najnowsza z nich, będąca największą ze znanych ludzkości liczb pierwszych, to 2^82589933 – 1. Jeżeli spróbujesz zapisać tę liczbę w układzie dziesiętnym, odkryjesz, że składa się ona z 28 862 048 cyfr, które z łatwością zapełnią około 10 000 stron książki.

Czy 1 jest liczbą pierwszą?

Nie. 1 nie jest liczbą pierwszą – chociaż często zdarza się, że uczniowie próbują podważać tę wersję. ☺ Aby dowieść, że 1 nie może być zakwalifikowana do zbioru liczb pierwszych, musimy cofnąć się do ich definicji.

Przypomnijmy: liczba pierwsza musi być podzielna przez dwie liczby – 1 i samą siebie. Nie mniej niż dwie i nie więcej niż dwie.

Jak jest w przypadku 1? Możemy podzielić ją tylko przez 1, a więc posiada ona tylko jeden dzielnik (nawet jeżeli jednocześnie spełnia on wymagania dla dwóch dzielników liczby pierwszej). Tym samym 1 nie spełnia definicji liczby pierwszej.

Czy 0 jest liczbą pierwszą?

Nie. 0 nie jest liczbą pierwszą, ponieważ liczba jego dzielników jest zdecydowanie większa niż 2 – jest ich nieskończenie wiele. ☺

Czym są liczby pierwsze bliźniacze?

W matematyce wyróżnia się kilka szczególnych rodzajów liczb pierwszych, m.in. liczby bliźniacze – liczby pierwsze, których różnica równa się 2. Spójrz na grafikę, którą przygotowaliśmy:

Wyjątkową liczbą pierwszą jest 5, które jest bliźniacze zarówno z 3, jak i z 7.

Jak wiele jest liczb pierwszych bliźniaczych? Niestety, wciąż tego nie wiemy. Istnieją hipotezy, według których liczb bliźniaczych jest nieskończenie wiele, jednak wciąż nie zdołano ich potwierdzić (lub ich obalić).

Ciekawostka
Oprócz liczb bliźniaczych, w matematyce istnieją również liczby pierwsze czworacze. Mianem tym określa się cztery liczby pierwsze, w przypadku których różnica między kolejnymi liczbami wynosi 2, 4, 2. Innymi słowy – są to dwie pary liczb bliźniaczych oddalonych od siebie o 4.

Przykładem liczb czworaczych jest 5, 7, 11, 13.

Zastosowanie liczb pierwszych – w życiu i w szkole

Liczby pierwsze znajdują zastosowanie przede wszystkim w informatyce. Przy ich użyciu tworzy się między innymi algorytmy szyfrowania danych, np. system RSA, umożliwiający bezpieczne przekazywanie wrażliwych informacji, takich jak numery kart kredytowych.

W szkole podstawowej liczby pierwsze wykorzystywane są do nieco mniej zaawansowanych działań. ☺ Ich znajomość będzie Ci niezbędna, aby rozłożyć dowolną liczbę złożoną na czynniki pierwsze. Rozkład liczb na czynniki pierwsze będzie Ci zaś potrzebny do tego, by:

wyznaczyć NWW – najmniejszą wspólną wielokrotność,
wyznaczyć NWD – największy wspólny dzielnik,
wyłączyć liczbę przed pierwiastek,
łatwo skracać liczby w ułamkach.

Jak widzisz, liczby pierwsze – oprócz tego, że są wyjątkowo ciekawe dla matematyków i naukowców – dają Ci przepustkę do nauki kolejnych, bardziej złożonych zagadnień. Kiedy je opanujesz, do kolejnych działów matematyki podejdziesz… na luzie!