Potęgi i działania na potęgach – mnożenie, dzielenie, potęgowanie potęg. Zadania i przykłady
Mogłoby się wydawać, że potęgi utrudniają życie i sprawiają, że lekcje matematyki są zdecydowanie trudniejsze. Nic bardziej błędnego! Potęgowanie to jedno z najbardziej wyluzowanych działań, z jakimi spotkasz się w szkole podstawowej. Dzięki potęgom możesz uprościć wiele obliczeń i oszczędzić sobie czasu na ich rozpisywanie. Nie wierzysz nam na słowo? Przeczytaj wpis, który dla Ciebie przygotowaliśmy i przekonaj się, że potęgi też mogą być na luzie.
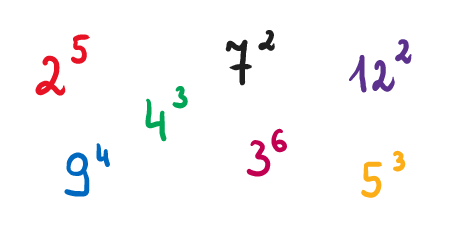
Czym są potęgi i gdzie można się z nimi spotkać?
Myślisz, że miejsce potęg jest w książce od matematyki, a nie w prawdziwym życiu? W takim razie popatrz na ten przykład:
Jesteś na siłowni i zamierzasz wykonać ćwiczenia, które przygotował dla Ciebie trener. Twój trening składa się z 6 ćwiczeń, z czego każde ćwiczenie należy wykonać w 6 seriach po 6 powtórzeń. Po powrocie do domu zastanawiasz się, ile powtórzeń łącznie udało Ci się wykonać. Oczywiście, możesz wykonać działanie 6*6*6, jednak równie dobrze możesz po prostu… podnieść 6 do 3 potęgi.
Wielokrotne mnożenie liczby przez siebie można zapisać w postaci potęgi.

Wniosek? Dzięki potęgowaniu możesz zwiększyć czytelność zapisu niektórych liczb i nieco ułatwić sobie życie. Dużo łatwiej (i przejrzyściej) jest zapisać 3*108 niż 300000000 lub 55 niż 5*5*5*5*5.
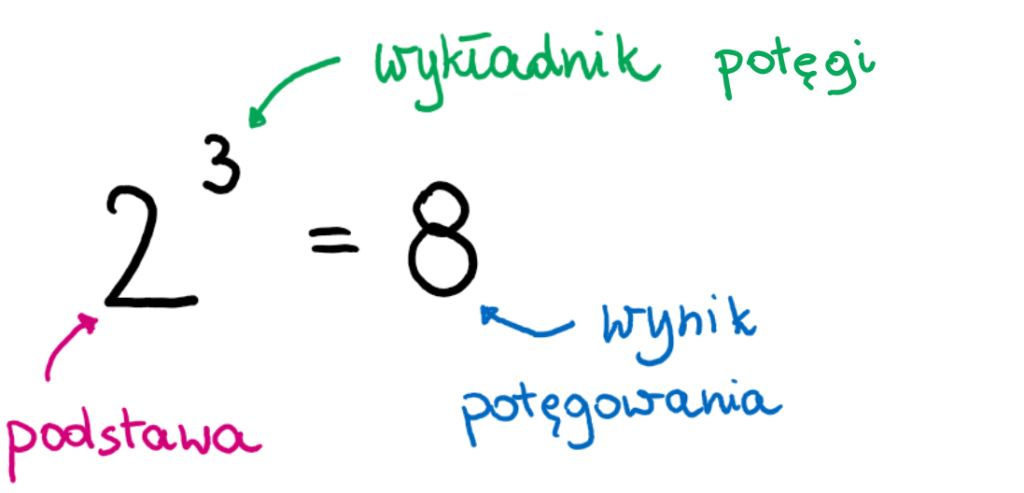
Jak nazywają się poszczególne elementy w potęgowaniu? Spójrz na grafikę:
Potęgi dodatnie i potęgi ujemne
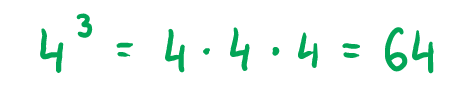
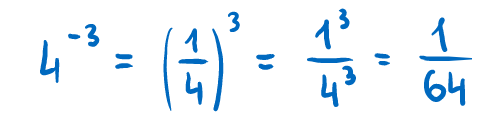
4 zostało obrócone do góry nogami i zmieniło się w ¼.
Potęgowanie liczb ujemnych
Podstawa potęgi może być liczbą ujemną. Jak postępować w takiej sytuacji? Wystarczy, że zapamiętasz prostą zasadę.
- Jeżeli wykładnik potęgi jest liczbą parzystą, wynik będzie liczbą dodatnią.
- Jeżeli wykładnik potęgi jest liczbą nieparzystą, wynik będzie liczbą ujemną.
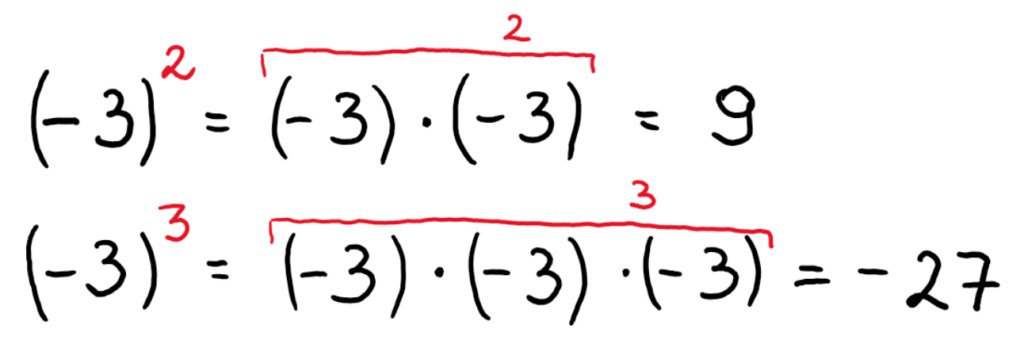
Działania na potęgach
Jak wygląda dodawanie i odejmowanie potęg? Najczęściej nie wygląda wcale, ponieważ w matematyce raczej nie wykonuje się tego typu działań (oczywiście istnieją pewne wyjątki od tej reguły, ale zanim do nich przejdziesz, musisz dobrze ogarniać podstawowe operacje).
Bardziej skomplikowane działania – takie jak mnożenie i dzielenie potęg – można w łatwy sposób upraszczać. Przykładowo, jeżeli chcesz wykonać mnożenie kilku potęg o takiej samej podstawie, to wystarczy, że dodasz do siebie ich wykładniki. Tak, jak zrobiliśmy to w poniższym przykładzie:
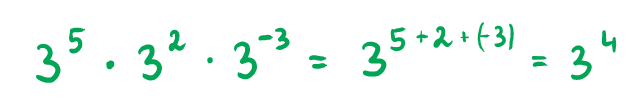
Operacje na wykładnikach można przeprowadzać zawsze wtedy, gdy mnożysz potęgi o tej samej podstawie, dzielisz potęgi o tej samej podstawie lub wykonujesz potęgowanie potęg. W zależności od działania, jakie wykonujesz, wykładniki należy dodać, odjąć lub pomnożyć.
Wszystkie działania na potęgach, rozdzielność potęg i potęgowanie potęg, omawiamy dokładnie w Matmie na Luzie dla klas 7-8. Aby wytłumaczyć zagadnienia związane z potęgowaniem, posłużyliśmy się treścią drukowaną, filmikami oraz rozszerzoną rzeczywistością. Wszystko na luzie, czyli w taki sposób, by nauka była łatwiejsza i jak najbardziej efektywna.
Jeżeli zamówisz MATMĘ NA LUZIE DLA KLAS 7-8 do godziny 11, to możesz ją otrzymać nawet jutro!
Aby przekonać się, w jaki sposób wykorzystuje się uproszczenia w działaniach na potęgach, spójrz na poniższy przykład:
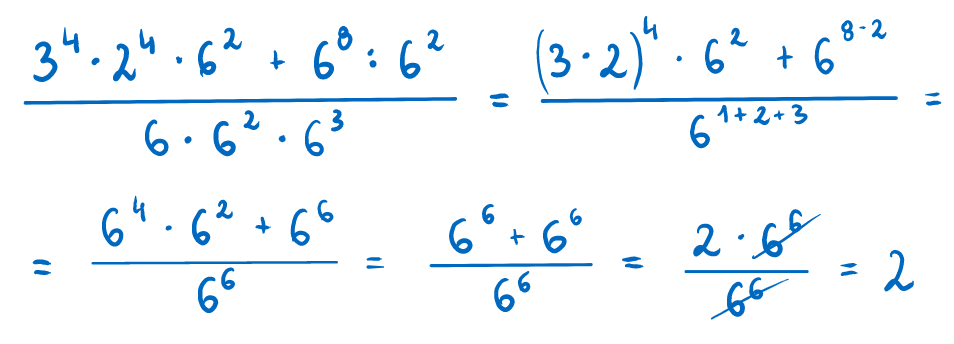
Notacja wykładnicza potęgi
Notacja wykładnicza to sposób zapisu bardzo dużych oraz bardzo małych liczb przy użyciu odpowiedniej potęgi liczby 10. Jak z niego korzystać? To naprawdę proste.
Aby zapisać liczbę w notacji wykładniczej, należy policzyć, o ile miejsc trzeba przesunąć przecinek, a następnie zapisać tę liczbę jako wykładnik przy liczbie 10. Tak, jak w poniższym przykładzie.
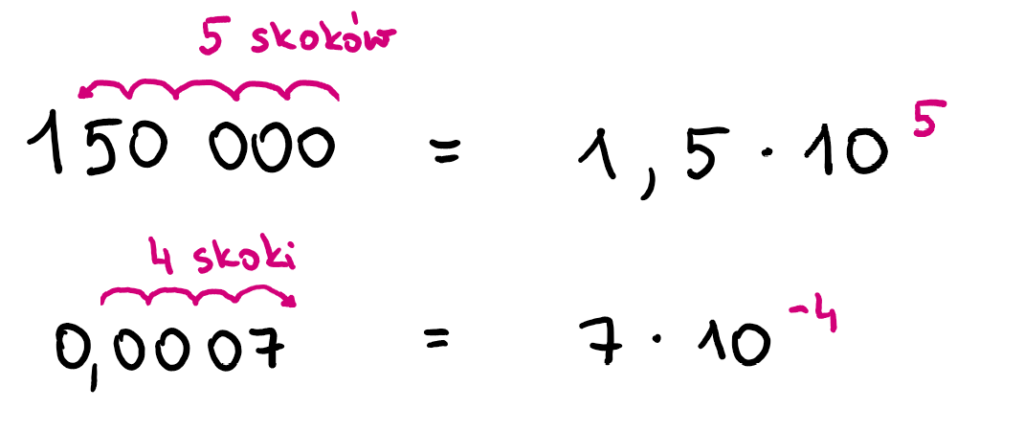
Przecinek należy przesunąć w taki sposób, by otrzymana liczba była większa lub równa 1, ale mniejsza od 10. Jeżeli przecinek przesuwamy w lewo, to wykładnik jest dodatni. Jeżeli przecinek przesuwany jest w prawo, wykładnik jest ujemny.
Co dalej? Kolejne kroki, jakie należy wykonać, by zapisać liczbę w postaci notacji wykładniczej, opisaliśmy w Matmie na Luzie. W naszej apce możesz przesuwać przecinek, aby zobaczyć, jak zmienia się wykładnik potęgi.
Potęgi – zadania do rozwiązania
Zadanie 1.
Twoja praca domowa składa się z 4 zadań. W każdym z nich znajdują się podpunkty od a do d. W każdym podpunkcie znajdują się 4 przykłady do rozwiązania.
Oblicz, ile przykładów łącznie musisz rozwiązać. Wynik zapisz w postaci potęgi, a następnie ją oblicz.
Zadanie 2. Uprość:
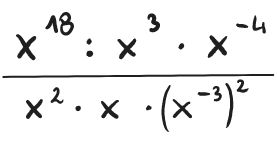
Zadanie 3. Oblicz:
25 + 23 * (-2)2
Potrzebujesz więcej wskazówek i dokładniejszych wyjaśnień?
Zajrzyj do Matmy na Luzie i ogarnij potęgi z rozszerzoną rzeczywistością w apce!
Zobacz także:

Egzamin ósmoklasisty 2026: matematyka w pytaniach i odpowiedziach. Jak przygotować się do testu? Zadania egzaminacyjne z matematyki
Egzamin ósmoklasisty – matematyka w pytaniach i odpowiedziach. Jak przygotować się do testu? Egzamin ósmoklasisty z matematyki zbliża się wielkimi krokami? Zachowaj spokój! Poniżej znajdziesz najważniejsze informacje na temat
Pola i obwody figur płaskich
Pola i obwody figur płaskich Bez względu na to, czy w Twoim obwodzie wychodzi się na pole czy na dwór, na lekcjach matematyki na pewno

Równanie z jedną niewiadomą – układanie i rozwiązywanie na przykładzie zadań
Równanie z jedną niewiadomą – układanie i rozwiązywanie na przykładzie zadań W matematyce wiele działów jest ze sobą powiązanych. Opanowanie jednego z nich otwiera Ci


