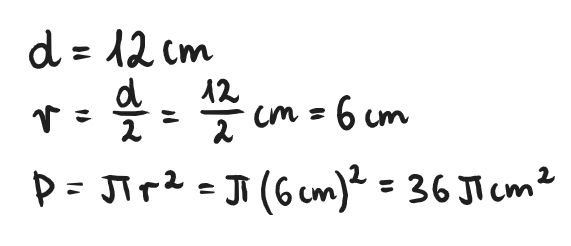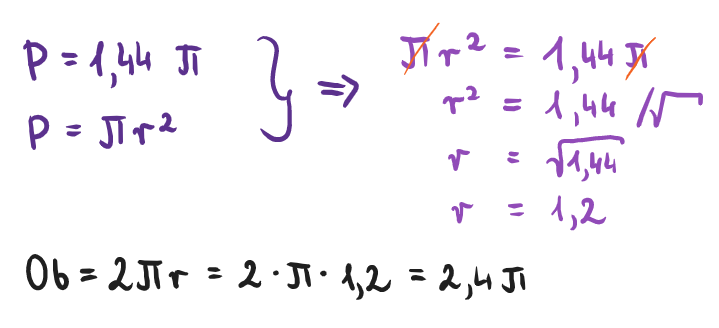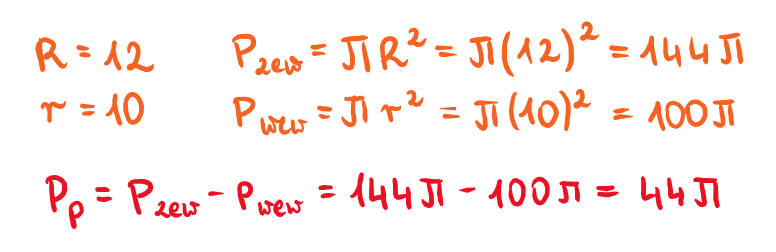Koło i okrąg – definicje, przykłady, zadania

Zdarza się, że pojęcia koła i okręgu bywają używane zamiennie. Na zajęciach sportowych możesz usłyszeć „zbierzmy się w okręgu”. Innym razem polecenie to brzmi „ustawcie się w kółku”. Można nabrać przekonania, że koło i okrąg to synonimy, jednak… w żadnym wypadku tak nie jest! Sprawdź, na czym polega różnica pomiędzy nimi, poznaj wzór na pole koła i rozwiąż zadania, które dla Ciebie przygotowaliśmy.

Koło a okrąg

Koło to figura geometryczna nieposiadająca kątów, z jedną krawędzią. Jego środek jest wypełniony – jak pizza. ☺ Każde koło posiada swój obwód, średnicę, promień oraz pole powierzchni. A Ty możesz obliczyć każdy z tych elementów.

W przeciwieństwie do koła, okrąg jest pusty w środku. Jest jedynie linią, brzegiem koła – możesz go sobie wyobrazić, jak hula hop. Jakie wartości możesz dla niego obliczyć? Jego promień, średnicę, a także długość. Uwaga: Długość okręgu jest równa obwodowi koła o tym samym promieniu.

Chcesz zobaczyć, czym okrąg różni się od koła? Zobacz film, który dla Ciebie przygotowaliśmy!

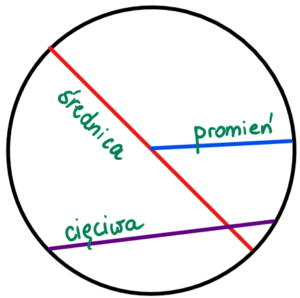
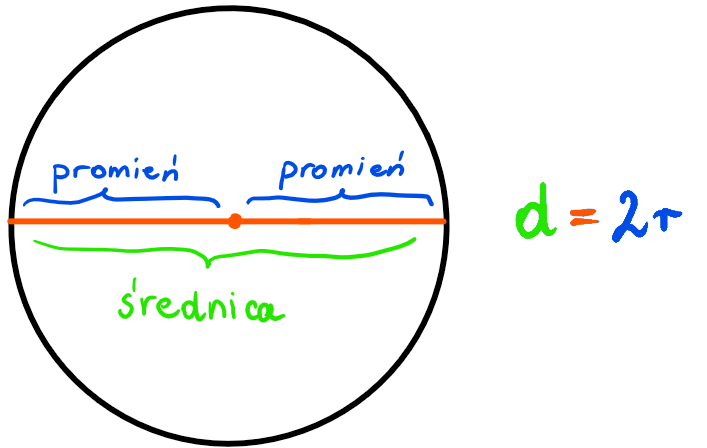
Czym są odcinki w kole?

Wyróżniamy trzy podstawowe rodzaje odcinków w kole. Są to:
  • Promień – odcinek, który łączy środek koła z dowolnym punktem na jego krawędzi (okręgu). Promień zawsze pozostaje taki sam – bez względu na to, jaki punkt na okręgu połączysz z punktem środkowym. Promień oznaczany jest w matematyce jako r lub R.
  • Średnica – odcinek, który łączy dwa punkty na krawędzi koła i przechodzi przez jego środek. Średnica oznaczana jest jako d lub D.
  • Cięciwa – odcinek, który łączy dwa dowolne punkty na okręgu. Cięciwa oznaczana jest jako c.

Promień i średnica – zależność pomiędzy odcinkami

Jeżeli znasz długość promienia lub średnicy koła – możesz z łatwością obliczyć długość drugiego odcinka. Jak to możliwe? Długość średnicy zawsze równa jest dwukrotności długości promienia.

Przykładowo, w kole, którego promień równy jest 7 cm, średnica będzie wynosić 14 cm. 

Spójrz na grafikę obok. 

Wzór na obwód koła

Obwód koła jest tym samym, czym długość okręgu. Aby go obliczyć, będziesz potrzebować następujących danych:

  • promień lub średnica koła
  • liczba π (Pi) – w przybliżeniu ma wartość 3,14.

Aby obliczyć obwód koła, skorzystaj z poniższego wzoru:

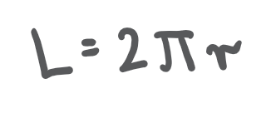
Wzór na pole koła

Pole powierzchni koła to przestrzeń, którą zajmuje koło (na powierzchni płaskiej).

Do obliczenia powierzchni koła, będzie Ci potrzebna:

  • długość promienia koła (pamiętaj, że możesz go samodzielnie obliczyć, jeżeli znasz średnicę!),
  • liczba π (Pi).

Aby obliczyć pole powierzchni koła, skorzystaj z poniższego wzoru:

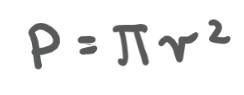
Liczba π (Pi) – co warto wiedzieć?

π jest liczbą niewymierną i stanowi tak zwaną stałą matematyczną. Pi ma nieskończenie wiele miejsc po przecinku.

π jest liczbą niewymierną i stanowi tak zwaną stałą matematyczną. Pi ma nieskończenie wiele miejsc po przecinku.

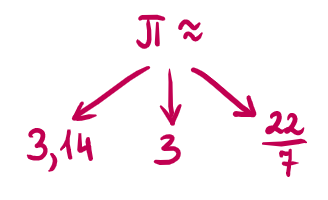
Do naszych obliczeń wystarczy przybliżenie:
π ≈ 3,14, a nawet π ≈ 3

W matematyce czasem wykorzystuje się podstawienia π ≈ 22/7 lub π ≈ 355/113, jednak to również nie jest dokładna wartość.

Liczba π wyraża stosunek długości okręgu (czyli obwodu koła) do długości jego średnicy. Co ważne, Pi znajduje zastosowanie przy każdym kole – niezależnie od jego rozmiarów – ponieważ, zgodnie z matematyczną zasadą, każde dwa koła są do siebie podobne.

Liczbę Pi wykorzystuje się do obliczeń geometrycznych, a także w analizie matematycznej, teorii liczb i w fizyce.

Czym jest pierścień kołowy?

Pierścień kołowy to przestrzeń pomiędzy dwoma okręgami, których środek znajduje się w tym samym miejscu. Brzmi niejasno? Spójrz na rysunek, który przygotowaliśmy:

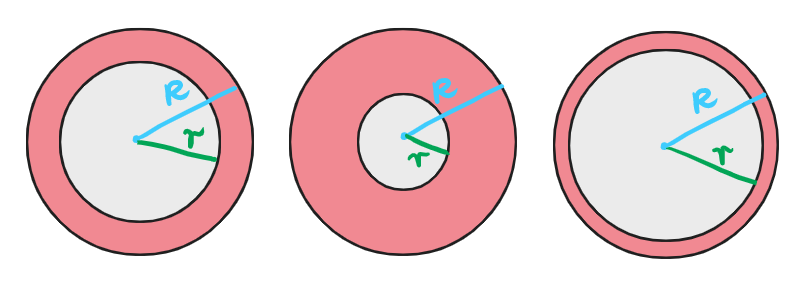
Aby ułatwić sobie rozwiązywanie zadań z pierścieniem kołowym, warto oznaczać promień zewnętrznego okręgu przy użyciu wielkiego R, a promień wewnętrznego okręgu przy użyciu małego r.

Do obliczenia powierzchni pierścienia kołowego należy:

  • obliczyć pole powierzchni zewnętrznego (dużego) koła,
  • obliczyć pole powierzchni wewnętrznego (mniejszego) koła,
  • odjąć wartość mniejszą (pole małego koła) od większej (pole dużego koła).

Koło i okrąg – zadania z rozwiązaniami

Czas, by sprawdzić swoją wiedzę! Rozwiąż zadania, które dla Ciebie przygotowaliśmy i porównaj swoje wyniki z naszymi odpowiedziami.

Zadanie 1
Oblicz pole powierzchni koła, którego średnica wynosi 12 cm. Nie podstawiaj przybliżenia w miejsce liczby π.

Zadanie 2 Oblicz obwód koła, którego pole wynosi 1,44 π. 

Zadanie 3
Oblicz pole pierścienia kołowego, mając do dyspozycji następujące dane:

  • zewnętrzny promień równy jest 12,
  • wewnętrzny promień równy jest 10.

Zobacz także: