Ułamki dziesiętne na luzie – działania na ułamkach dziesiętnych
Ułamki to podstawa szkolnej matematyki. Są jak deklinacja rzeczowników na języku polskim, czy przewrót w przód na wuefie. Dopóki ich nie opanujesz, nie ruszysz z nauką do przodu. Dlatego warto poświęcić im nieco uwagi!
W tym wpisie zajmujemy się ułamkami dziesiętnymi – omawiamy działania na ułamkach, porównywanie i zaokrąglanie ułamków dziesiętnych. Jak zawsze na luzie!

Ułamki dziesiętne – czym są i jak wyglądają?
Jak sama nazwa wskazuje, ułamek jest częścią liczby – ułamanym fragmentem całości. Na lekcjach matematyki spotkasz się z dwoma rodzajami ułamków: ułamkami zwykłymi oraz dziesiętnymi.
Ułamki zwykłe zapisuje się przy użyciu kreski ułamkowej, która oddziela licznik i mianownik.
Ułamki dziesiętne zapisuje się bez kreski. Znakiem, który pozwala je rozpoznać, jest przecinek dziesiętny. Przecinek dzieli liczbę na dwie części – to, co znajduje się przed nim, odpowiada części całkowitej. To, co znajduje się za przecinkiem, odpowiada części ułamkowej.
Ciekawostka: w USA, Wielkiej Brytanii i pozostałych krajach anglosaskich ułamki dziesiętne zapisuje się z wykorzystaniem kropki zamiast przecinka.
Jak czytać ułamki dziesiętne?
Nazwa ułamka dziesiętnego związana jest z ostatnim miejscem, na którym znajduje się cyfra inna niż zero.
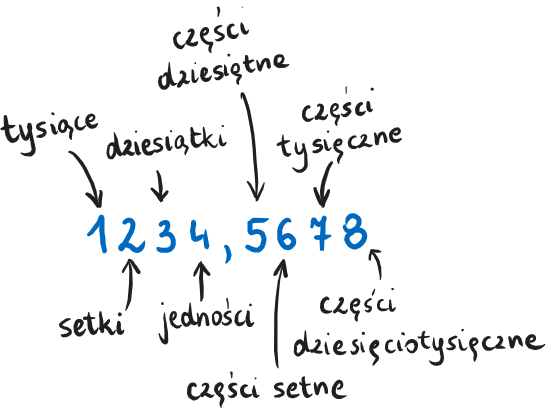
- 2,6 czytamy jako dwa i sześć dziesiątych,
- 7,24 czytamy jako siedem i dwadzieścia cztery setne,
- 102,715 czytamy jako sto dwa i siedemset piętnaście tysięcznych
Porównywanie ułamków dziesiętnych
Porównywanie ułamków dziesiętnych nie różni się znacząco od porównywania liczb całkowitych.
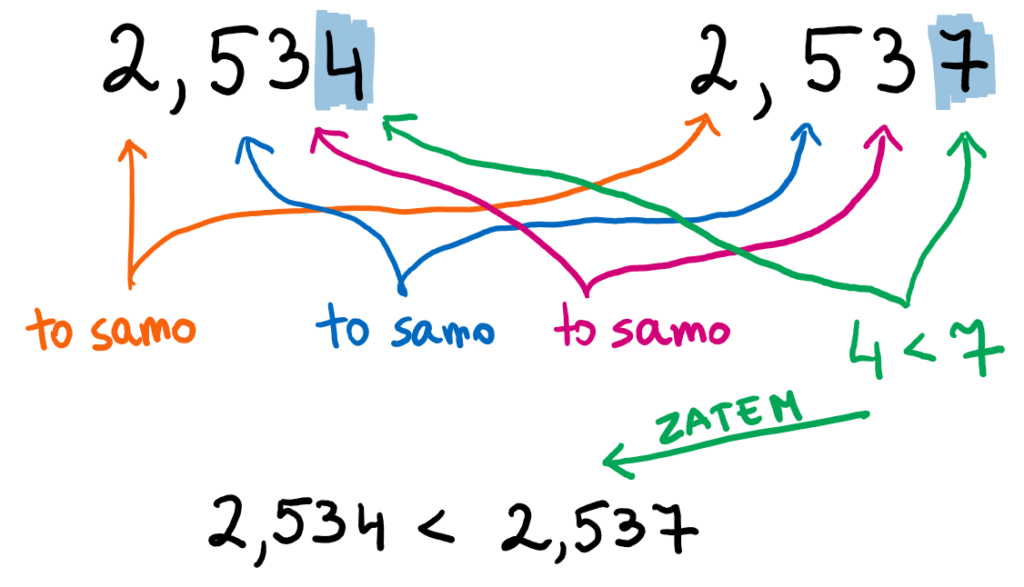
Pamiętaj, by porównywać cyfry znajdujące się za tymi, które są takie same.
Spójrz na przykład:
Działania na ułamkach dziesiętnych -dodawanie, odejmowanie, zaokrąglanie
Dodawanie i odejmowanie ułamków dziesiętnych
Ułamki dziesiętne można dodawać i odejmować na luzie, o ile pamiętasz o jednej kluczowej zasadzie. Oto ona:
zawsze dodawaj i odejmuj cyfry, które znajdują się na tych samych miejscach dziesiętnych!
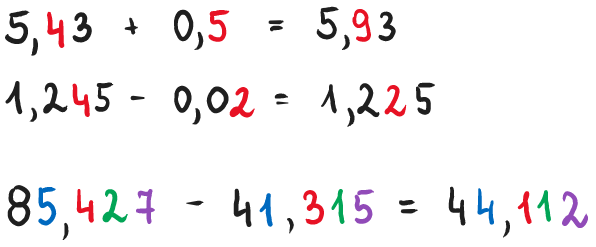
Co z bardziej skomplikowanymi ułamkami? Aby przeprowadzić trudniejsze działania, możesz skorzystać z działania pisemnego. Pamiętaj jednak, aby zawsze zapisać przecinek pod przecinkiem. Tak jak w przykładzie, który dla Ciebie przygotowaliśmy.
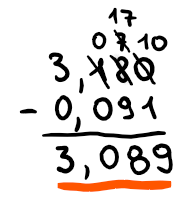
Dzielenie ułamków dziesiętnych, mnożenie ułamków dziesiętnych
Ważne! Mnożenie i dzielenie ułamków dziesiętnych (w tym działania pisemne na ułamkach dziesiętnych) dokładnie opisaliśmy w Matmie na Luzie. Sięgnij po naszą książkę z appką, aby dowiedzieć się więcej na ten temat.
Zaokrąglanie ułamków dziesiętnych
W zaokrąglaniu ułamków dziesiętnych stosuje się tę samą zasadę, co w przypadku liczb całkowitych. A zatem należy:
- podkreślić ostatnią cyfrę, która nie jest zerem
- spojrzeć na kolejną cyfrę
- jeżeli jest mniejsza niż 5, zaokrąglić w dół
- jeżeli jest równa lub większa od 5, zaokrąglić w górę
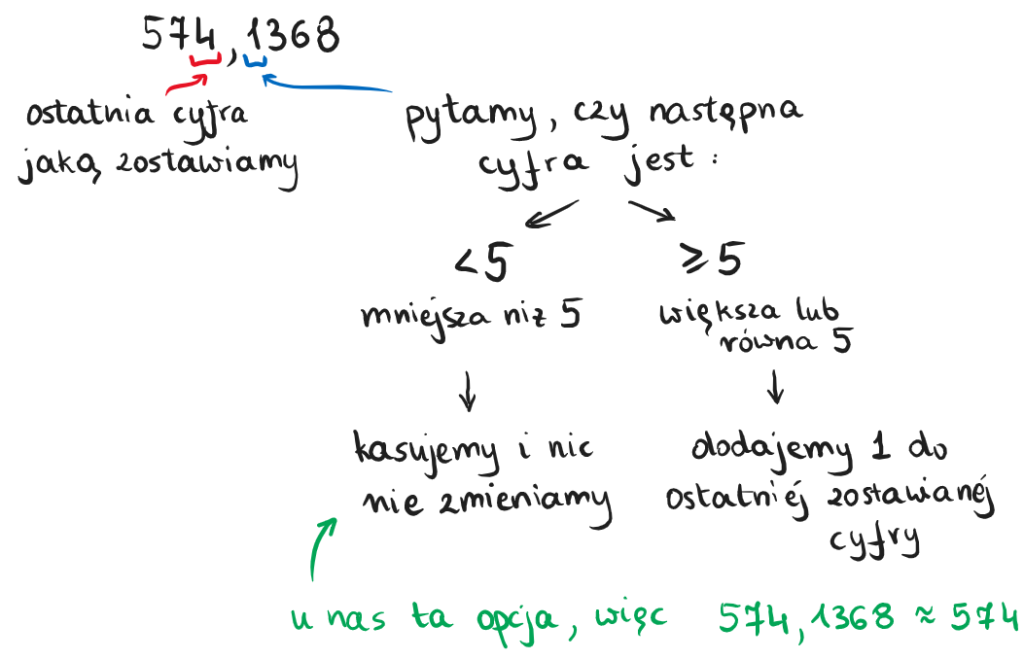
Rozwiązując zadania, często można spotkać się z poleceniem zaokrąglij do drugiego miejsca po przecinku. W takim wypadku zwykle nie ma wątpliwości, w którym miejscu należy wykonać działanie.
Nieco trudniej bywa wtedy, gdy zadanie brzmi zaokrąglij do części tysięcznych. Jeżeli spotkasz się z takim poleceniem, przypomnij sobie grafikę z początku tego działu – pomoże Ci ona rozszyfrować, o które miejsce po przecinku chodzi.
Działania na ułamkach zwykłych i dziesiętnych
Często zdarza się, że trzeba wykonać działania, w których ułamki zwykłe przeplatają się z ułamkami dziesiętnymi. Nie tylko w szkole, ale również w codziennych czynnościach.
Wyobraź sobie, że pieczesz ciasto. W przepisie znajdujesz informację dodaj ¼ kostki masła. Zerkasz na opakowanie, na którym znajdujesz informację, że kostka waży 0,2 kg. Jaką ilość masła należy dodać?
Aby poradzić sobie w takiej sytuacji, musisz zdecydować, jakim rodzajem ułamków chcesz operować, a następnie zamienić wszystkie z nich na dziesiętne lub zwykłe.
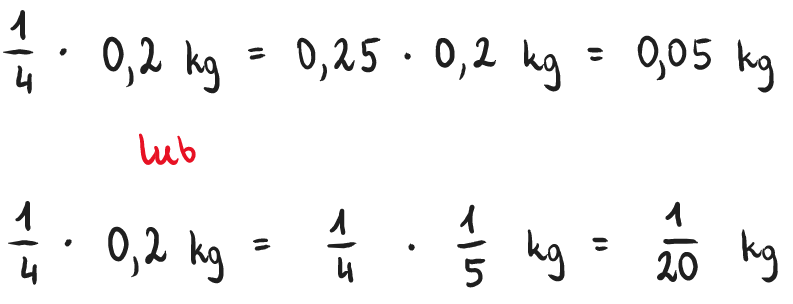
Co ważne, nie ma jednego, uniwersalnego przepisu na takie okazje. Czasami łatwiej jest zamienić ułamek dziesiętny na zwykły, a czasem zwykły na dziesiętny. Wszystko zależy od konkretnego przypadku.
Ważne! Nie pamiętasz, jak zamieniać ułamki dziesiętne na zwykłe i na odwrót? Zerknij do wpisu Ułamki zwykłe bez tajemnic oraz do naszej książki Matma na Luzie, w której tłumaczymy wszystko od A do Z.
Ułamki dziesiętne - zadania
Zadanie 1. Porównaj ułamki: 19,245 oraz 19,25.
Odpowiedzi do zadania
Zadanie 1
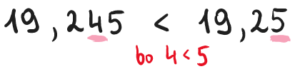
Zadanie 2
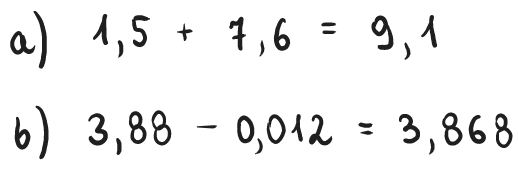
Zadanie 3

Zadanie 4
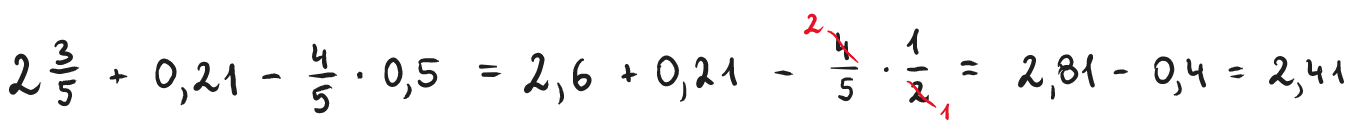
Potrzebujesz więcej wskazówek i dokładniejszych wyjaśnień?
Zajrzyj do Matmy na Luzie i ogarnij ułamki dziesiętne z rozszerzoną rzeczywistością w apce!
Zobacz także:

Egzamin ósmoklasisty 2026: matematyka w pytaniach i odpowiedziach. Jak przygotować się do testu? Zadania egzaminacyjne z matematyki
Egzamin ósmoklasisty – matematyka w pytaniach i odpowiedziach. Jak przygotować się do testu? Egzamin ósmoklasisty z matematyki zbliża się wielkimi krokami? Zachowaj spokój! Poniżej znajdziesz najważniejsze informacje na temat
Pola i obwody figur płaskich
Pola i obwody figur płaskich Bez względu na to, czy w Twoim obwodzie wychodzi się na pole czy na dwór, na lekcjach matematyki na pewno

Równanie z jedną niewiadomą – układanie i rozwiązywanie na przykładzie zadań
Równanie z jedną niewiadomą – układanie i rozwiązywanie na przykładzie zadań W matematyce wiele działów jest ze sobą powiązanych. Opanowanie jednego z nich otwiera Ci


