Rodzaje kątów i ich miary – garść wiedzy o kątach
Rodzaje kątów i ich miary – garść wiedzy o kątach Ostre, proste, rozwarte, wklęsłe i wypukłe… Kąty przyprawiają Cię o zawroty głowy? Zanim rzucisz zeszyt
Ostrosłupy na luzie – teoria i zadania
Ostrosłupy czasem dają ostro popalić… Ale nie musi tak być! Zamiast załamywać ręce nad zeszytem do matmy, wyluzuj się i skorzystaj z naszych podpowiedzi. Już za chwilę dostaniesz porcję zrozumiałej teorii o ostrosłupach: dowiesz się, czym jest ostrosłup prawidłowy, jak oblicza się pole powierzchni ostrosłupa, czym różnią się od siebie ostrosłup trójkątny i ostrosłup czworokątny i jeszcze więcej! Na końcu wpisu zamieściliśmy kilka zadań, dzięki którym przetestujesz zdobytą wiedzę w praktyce. Gotowy/a? Zaczynamy. ☺
Co to jest ostrosłup?
First things first – czym są ostrosłupy? Czy to ostro zakończone słupy? Spójrz na definicję, którą dla Ciebie przygotowaliśmy.
Ostrosłupy to figury przestrzenne, które mają jedną podstawę, a ich ściany boczne są trójkątami. Ściany boczne zbiegają się w jednym punkcie, który nazywamy wierzchołkiem ostrosłupa.
Z czego składają się ostrosłupy?
Przyjrzyjmy się bliżej elementom ostrosłupa. Spójrz na grafikę:
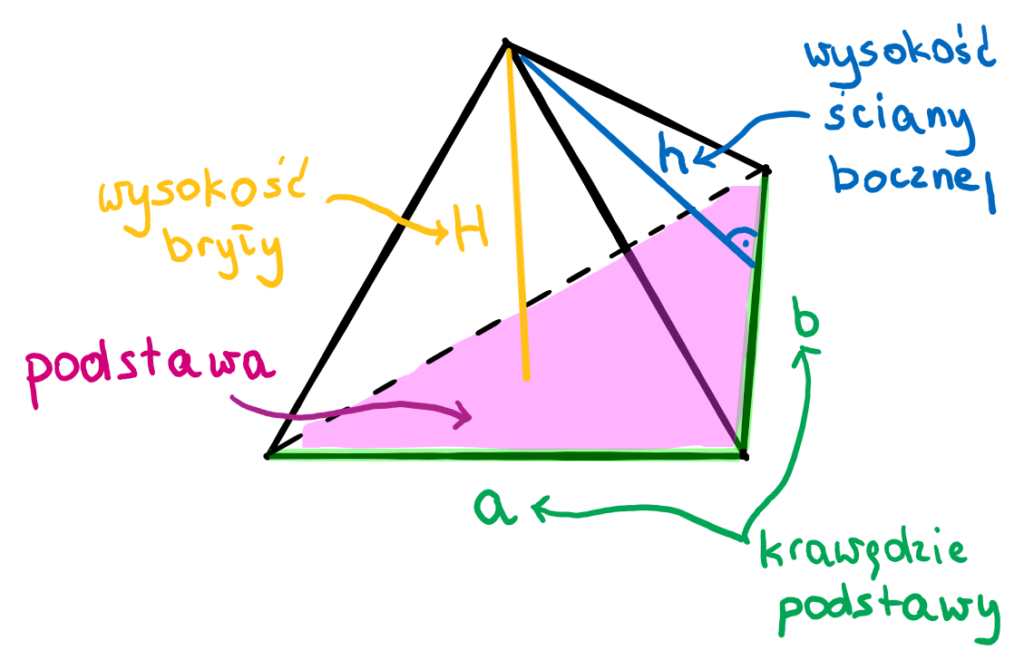
Zauważ, gdzie znajdują się takie elementy ostrosłupa, jak podstawa i ściany boczne. Spójrz, gdzie należy szukać krawędzi podstawy, wysokości ściany bocznej czy wysokości bryły.
PROTIP:
W apce Matma na Luzie dla klas 7-8 możesz obejrzeć wszystkie elementy ostrosłupa w 3D.
Rodzaje ostrosłupów ze względu na figurę w podstawie
Każdy ostrosłup ma jedną podstawę, którą stanowi określona figura, np. trójkąt, czworokąt, sześciokąt.
Nazwa ostrosłupa najczęściej powiązana jest z figurą, która znajduje się w jego podstawie. Oto kilka przykładów:
- Ostrosłup trójkątny – to figura, która ma w podstawie trójkąt.
- Ostrosłup czworokątny – to figura, która ma w podstawie czworokąt.
- Ostrosłup pięciokątny – to figura, która ma w podstawie pięciokąt.
Zobacz je na poniższej grafice:
Ostrosłup prawidłowy, czyli jaki?
Ostrosłup prawidłowy to ostrosłup, który ma w podstawie wielokąt foremny. Ale… zaraz, zaraz. Czym jest wielokąt foremny? Przypomnijmy!
Mianem wielokąta foremnego określamy figurę geometryczną, której wszystkie boki mają taką samą długość, a wszystkie kąty mają takie same miary. Do wielokątów foremnych zaliczamy m.in. trójkąt równoboczny. A zatem:
- Ostrosłup prawidłowy trójkątny ma w podstawie trójkąt równoboczny.
- Ostrosłup prawidłowy czworokątny ma w podstawie kwadrat.
- Ostrosłup prawidłowy pięciokątny ma w podstawie pięciokąt foremny.
Wszystko jasne? W takim razie ruszajmy dalej.
Pole powierzchni ostrosłupa – jak je obliczyć?
Pole powierzchni całkowitej to suma pól wszystkich ścian bryły. Innymi słowy, jest to pole opakowania, w jakim znajduje się bryła – w tym wypadku ostrosłup. W zadaniach pole powierzchni całkowitej oznacza się jako Pc .
Pole powierzchni całkowitej zazwyczaj oblicza się poprzez dodanie do siebie pola podstawy i pola bocznego.
Pole podstawy to pole figury, która znajduje się w podstawie ostrosłupa. W zadaniach oznacza się je symbolem Pp . Pole boczne to suma pól wszystkich ścian bocznych. Oznaczamy je jako Pb .
Wzór na pole powierzchni całkowitej przestawia się zatem w następujący sposób:
Czym jest objętość ostrosłupa i jak ją obliczyć?
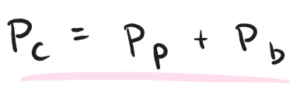
Przy pomocy objętości możemy określić wypełnienie bryły, czyli to, co znajduje się we wspomnianym wcześniej opakowaniu. Określając objętość, możemy odpowiedzieć na pytanie, jak wiele mieści się w jej środku.
W zadaniach objętość oznacza się jako V.
Aby obliczyć objętość ostrosłupa, należy pomnożyć pole podstawy przez wysokość ostrosłupa, a następnie podzielić wynik przez 3.
Spójrz na wzór:
Szczególne przykłady ostrosłupów
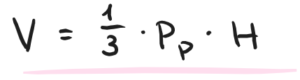
Czas na ciekawostki. W matematyce wyróżniamy kilka wyjątkowych ostrosłupów, ale największą gwiazdą wśród nich jest czworościan foremny. Co odróżnia go od reszty?
Czworościan foremny to ostrosłup, którego wszystkie ściany – zarówno ściany boczne, jak i podstawa – są trójkątami równobocznymi.
Chcesz zobaczyć, jak wygląda czworościan foremny? Spójrz na rysunek, na którym opisaliśmy wzory na obliczenie objętości, pola podstawy, pola bocznego oraz pola powierzchni całkowitej w tym wyjątkowym ostrosłupie.
Ostrosłupy – zadania do rozwiązania
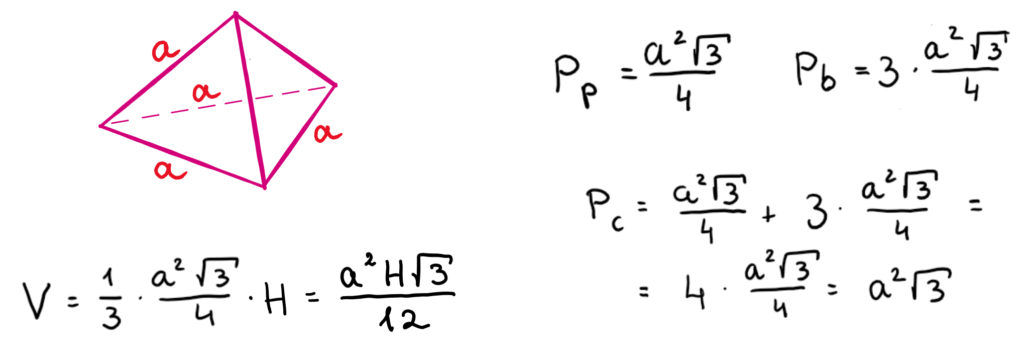
Czas, by sprawdzić swoją wiedzę w praktyce. Rozwiąż zadania, które dla Ciebie przygotowaliśmy.
Zadanie 1. Podstawa pewnego ostrosłupa prawidłowego jest kwadratem o boku 6 cm. Jego ściana boczna jest trójkątem równoramiennym o ramieniu długości 5 cm. Oblicz pole powierzchni całkowitej tego ostrosłupa.
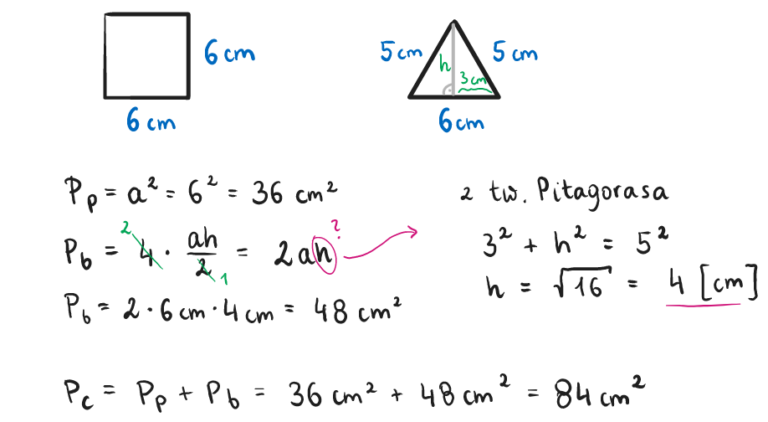
Zadanie 2. Pole powierzchni bocznej ostrosłupa prawidłowego czworokątnego wynosi 1040 cm2. Jego podstawa ma pole 400 cm2. Oblicz, ile wynosi wysokość ściany bocznej tego ostrosłupa.
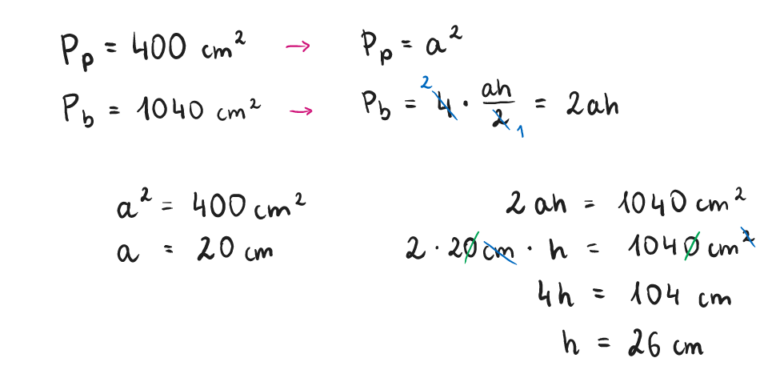
Zadanie 3. Oblicz objętość czworościanu foremnego, jeśli jego pole całkowite wynosi 81√3, a wysokość 3√6.
MATMA NA LUZIE – doskonała alternatywa lub uzupełnienie korepetycji z matematyki
Zobacz także:
Przystawanie trójkątów – kluczowe pojęcia dla ósmoklasisty
Przystawanie trójkątów – kluczowe pojęcia dla ósmoklasisty Przystawanie trójkątów to temat, który przystoi poznać. Jako jedno z najważniejszych pojęć geometrii pojawia się nie tylko na
Jak obliczyć całkowity koszt wyjazdu, czyli matma na wakacjach.
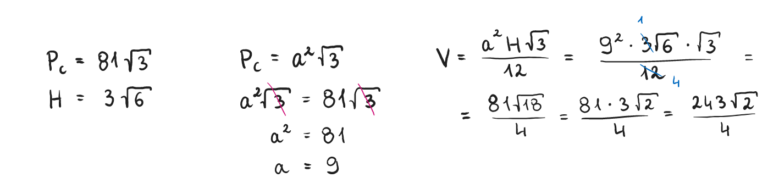
Jak obliczyć całkowity koszt wyjazdu, czyli matma na wakacjach Latem można odpocząć od szkoły, ale nie od matmy – zwłaszcza jeżeli chcesz zaplanować budżet na