Twierdzenie Pitagorasa – definicja, przykłady, zadania i kilka ciekawostek
Twierdzenie Pitagorasa to jedno z najważniejszych twierdzeń, z jakimi zetkniesz się na lekcjach matematyki. Przy jego pomocy obliczysz długość jednego z boków trójkąta prostokątnego – oczywiście o ile znasz długość pozostałych dwóch. Jak brzmi twierdzenie Pitagorasa? Kto był jego prawdziwym autorem? Sprawdzamy!
Twierdzenie Pitagorasa – historia i kontrowersje
Pytanie kto jest autorem twierdzenia Pitagorasa? Może wydawać się absurdalne, jednak… jest w pełni uzasadnione.
Kultura zachodnioeuropejska powiązała twierdzenie a2+b2=c2 z greckim matematykiem i filozofem, żyjącym w VI w p.n.e. – Pitagorasem. Historycy udowadniają, że niesłusznie! Za najbardziej prawdopodobne miejsce powstania twierdzenia uznaje się Babilonię (starożytne państwo Mezopotamii, położone na terenie współczesnego Iraku). Tamtejsi matematycy mieli opracować kilka metod, które pozwalały obliczyć długość trzeciego boku trójkąta prostokątnego – w tym co najmniej dwie znacznie prostsze od twierdzenia Pitagorasa, ale są mniej dokładne.
Co ciekawe, twierdzeniem a2+b2=c2 prawdopodobnie posługiwano się również w starożytnym Egipcie, Chinach i Indiach. Na długo przed narodzinami Pitagorasa. 
MATMA NA LUZIE
dla klas 7-8
Rewolucyjny sposób na naukę z rozszerzoną rzeczywistością (AR)
- przygotowanie do egzaminu ósmoklasisty
- pomaga w samodzielnym uczeniu się
- 23 działy zgodne z podstawą programową
- skorzystało ponad 6700 uczniów
Warto wiedzieć
- dowód twierdzenia Pitagorasa,
- stworzenie pierwszej klasyfikacji liczb (obejmującej m.in. liczby parzyste i nieparzyste, pierwsze, doskonałe, będące kwadratami),
- udowodnienie, że suma kątów w trójkącie wynosi 180 stopni,
- wprowadzenie pojęcia średniej arytmetycznej,
- opracowanie konstrukcji wielościanów foremnych,
- odkrycie dwunastościanu foremnego.
Twierdzenie Pitagorasa – wzór
Twierdzenie Pitagorasa stosuje się tylko i wyłącznie w odniesieniu do trójkątów prostokątnych. Zgodnie z jego założeniami, w każdym trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej. Wzór twierdzenia wygląda następująco:
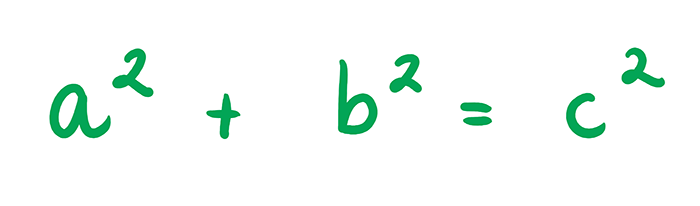
Z czego:
- a i b to długości przyprostokątnych, czyli boków trójkąta, które leżą bezpośrednio przy kącie prostym;
- c to długość przeciwprostokątnej, czyli boku trójkąta, który położony jest naprzeciwko kąta prostego.
Dowody twierdzenia Pitagorasa
Każde matematyczne twierdzenie potrzebuje solidnych dowodów. Nie inaczej było w przypadku twierdzenia Pitagorasa! Na przestrzeni wieków opublikowano wiele ponad 100 dowodów na poprawność twierdzenia – pierwszy z nich został prawdopodobnie opracowany przez Pitagorasa (lub jednego z jego uczniów). Niektórzy matematycy twierdzą, że kolejne dowody można opracowywać nieustannie, ponieważ jest ich nieskończenie wiele.
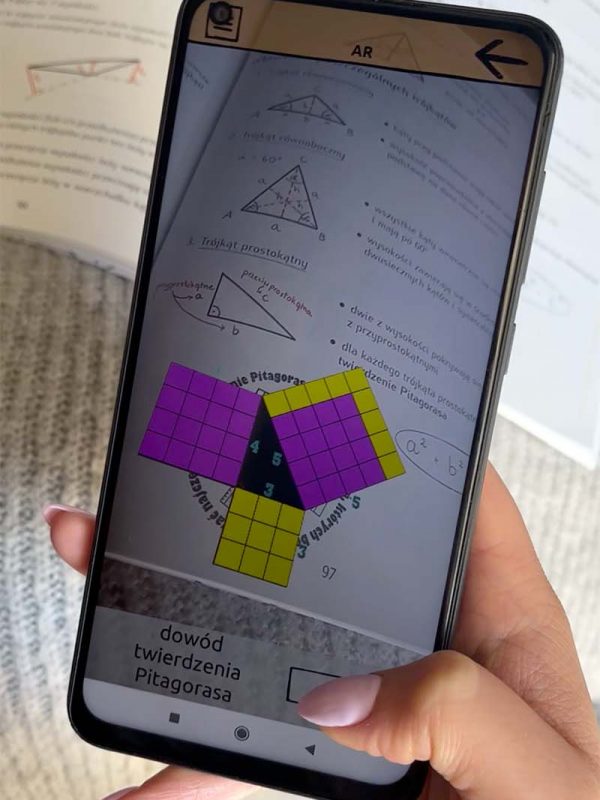
Poniżej prezentujemy jeden z najpopularniejszych dowodów twierdzenia Pitagorasa. W naszym zestawie MATMA NA LUZIE DLA KLAS 7-8 wyjaśniamy dowód wykorzystując rozszerzoną rzeczywistość.
Na każdym z boków trójkąta zbudowano kwadraty, a następnie podzielono je na mniejsze kwadraciki o identycznych wymiarach. Zwróć uwagę, że kwadraciki z przyprostokątnych odpowiadają sumie kwadracików, jakie znalazły się na przeciwprostokątnej. Teraz chyba już nie masz wątpliwości, że twierdzenie Pitagorasa jest zgodne z prawdą?
Twierdzenie Pitagorasa – ciakawostki
Na podstawie twierdzenia Pitagorasa stworzono definicję trójkąta pitogarejskiego:
Trójkąt pitagorejski to trójkąt o bokach wyrażonych liczbami naturalnymi a, b, c, spełniającymi warunek a2+b2=c2.
Jak łatwo się domyślić, trójkątem pitagorejskim jest trójkąt prostokątny. ☺
Aby odnaleźć trójkąty pitagorejskie, można posłużyć się wzorem stworzonym przez Pitagorasa:
a=2n+1
b=2n(n+1)
c=2n2+2n+1
Szczególnym rodzajem trójkąta pitogarejskiego jest trójkąt egipski – jest to jedyny trójkąt, który spełnia warunek a2+b2=c2, a przy tym posiada boki o długościach odpowiadających kolejnym liczbom naturalnym: 3, 4 i 5. W starożytnym Egipcie wykorzystywano go do wyznaczania kątów prostych, np. wyznaczaniu granic ziem, które regularnie zacierane były przez wodę z Nilu.
Twierdzenie Pitagorasa – zastosowanie
- Obliczenia długości trzeciego boku trójkąta prostokątnego – w sytuacji, gdy znane są długości dwóch boków. Wystarczy, że skorzystasz ze wzoru a2+b2=c2.
- Sprawdzenia, czy trójkąt jest prostokątny. W sytuacji, gdy znane są długości wszystkich boków, wystarczy, że wstawisz je do wzoru i potwierdzisz ich zależność.
Twierdzenie Pitagorasa – przykłady
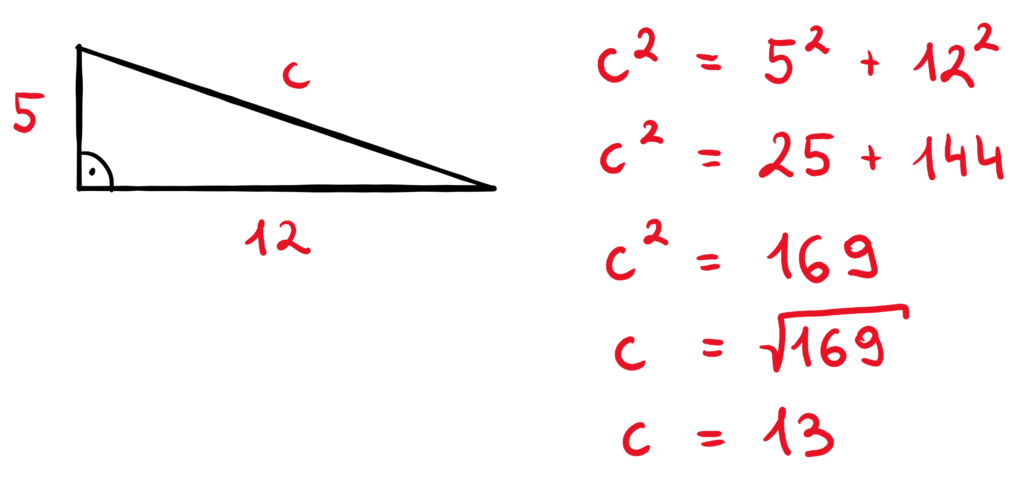
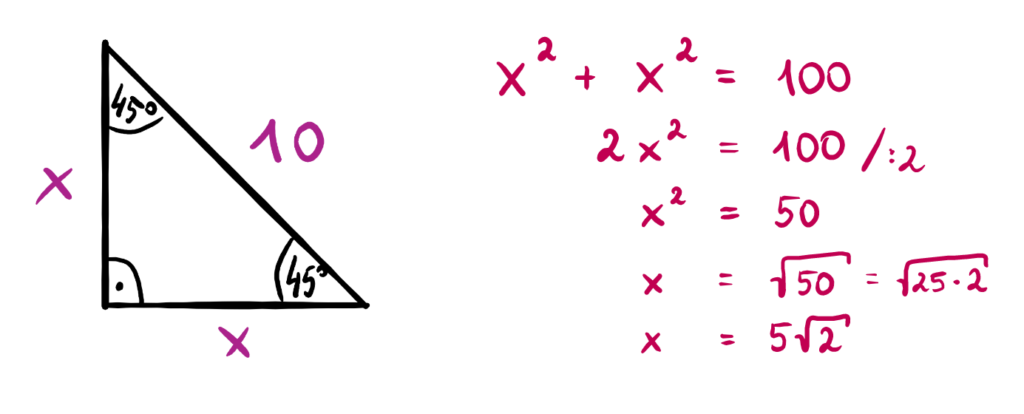
Sprawdzian z twierdzenia Pitagorasa
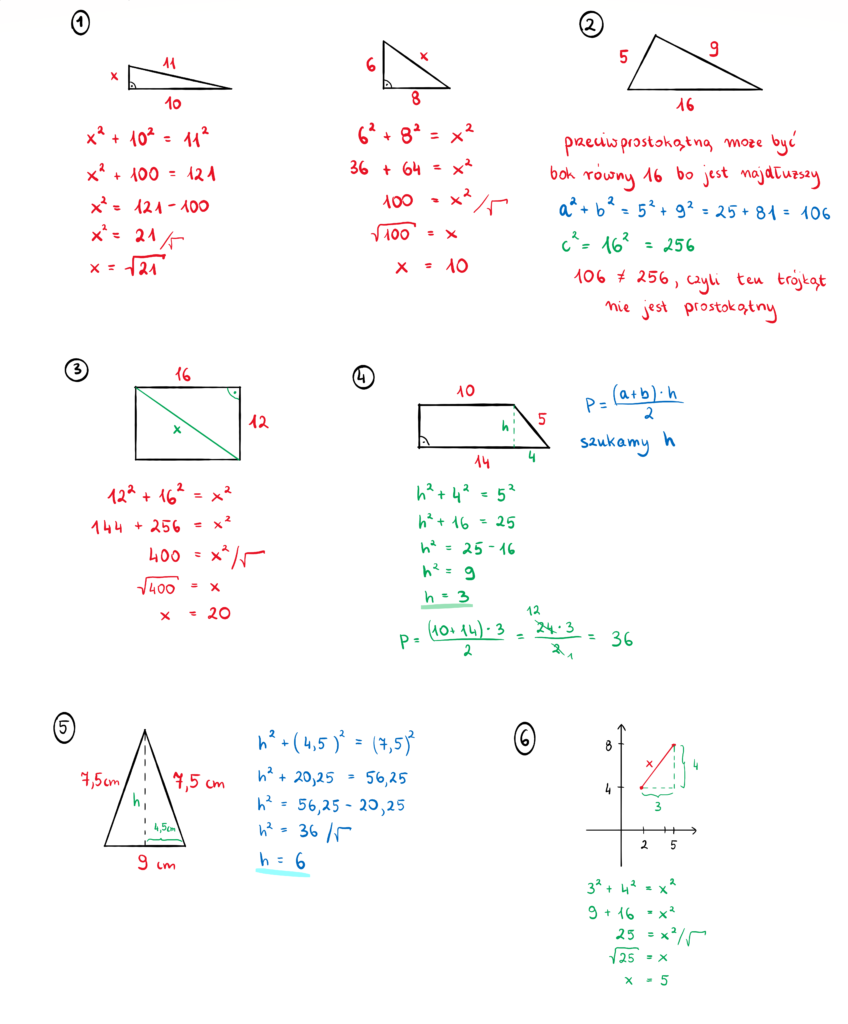
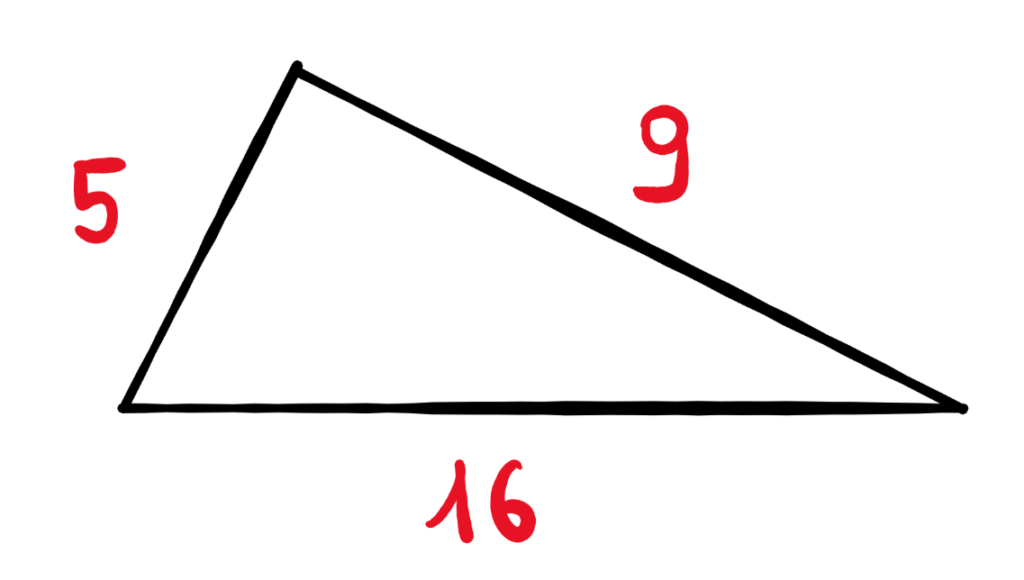
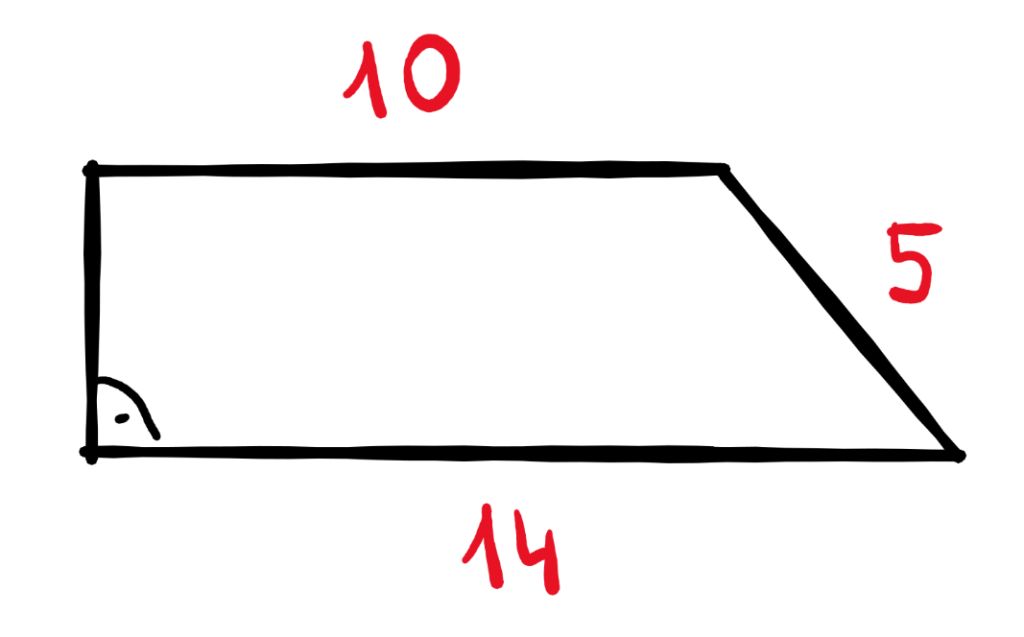
Zadanie 1. Oblicz długość boku oznaczonego jako x:
Zadanie 5.
Oblicz wysokość w trójkącie równoramiennym o bokach długości:
- 7,5 cm
- 7,5 cm
- 9 cm
Zadanie 6.
Oblicz długość odcinka AB w układzie współrzędnych.
Współrzędne punktów to:
- A (5,8)
- B (2,4)
Zobacz także:
Rodzaje kątów i ich miary – garść wiedzy o kątach
Rodzaje kątów i ich miary – garść wiedzy o kątach Ostre, proste, rozwarte, wklęsłe i wypukłe… Kąty przyprawiają Cię o zawroty głowy? Zanim rzucisz zeszyt
Przystawanie trójkątów – kluczowe pojęcia dla ósmoklasisty
Przystawanie trójkątów – kluczowe pojęcia dla ósmoklasisty Przystawanie trójkątów to temat, który przystoi poznać. Jako jedno z najważniejszych pojęć geometrii pojawia się nie tylko na
Jak obliczyć całkowity koszt wyjazdu, czyli matma na wakacjach.
Jak obliczyć całkowity koszt wyjazdu, czyli matma na wakacjach Latem można odpocząć od szkoły, ale nie od matmy – zwłaszcza jeżeli chcesz zaplanować budżet na
Twierdzenie Pitagorasa – odpowiedzi do zadań
